9.1 – Los tipos de contadores
En electrónica digital debemos separar los circuitos lógicos sin ninguna sincronización, de aquellos que tienen algún tipo de sincronización externa, sea, utilizar una señal de CLOCK.
Hay, por lo tanto, circuitos que caen en lo que se llama lógica simple y en lo que se llama lógica sincronizada.
Lo que pasa es que hay aplicaciones donde, todo lo que le importa al circuito, es hacer una operación con ciertos niveles lógicos aplicados a su entrada cuando están presentes, no siendo importante el momento en que se produce.
Tales circuitos no necesitan ninguna sincronización y son más simples de utilizar.
Sin embargo, con circuitos muy complejos, como los utilizados en ordenadores, máquinas industriales, instrumentos electrónicos y dispositivos de mecatrónica, además de muchos otros casos, el instante en que se debe realizar una operación es muy importante, y esto implica que los circuitos deben estar habilitados en el instante exacto en que se aplican ciertos niveles lógicos a su entrada.
Esto significa que estos circuitos deben estar sincronizados por algún tipo de señal procedente de un circuito externo. Este circuito no es más que un oscilador que produce una señal de clock o reloj.
Los circuitos que operan con estas señales se denominan circuitos con lógica sincronizada.
Para los contadores, entonces tenemos varias clasificaciones que toman este factor y otros en cuenta, por ejemplo:
a) Clasificación cuanto al Sincronismo:
Los contadores pueden ser ASINCRÓNICOS, cuando la señal del clock se aplica solamente a la primera etapa. Las etapas siguientes utilizan como señal de sincronización la salida de cada etapa anterior. Estos contadores también se llaman " Ripple Counters ".
El término inglés se utiliza normalmente, incluso en documentos en español, como con muchos otros términos técnicos, como ya hemos advertido a nuestros lectores.
Los contadores pueden también ser SÍNCRONOS o SINCRONIZADOS cuando hay una sola señal externa del clock, que se aplica a todas las etapas al mismo tiempo.
En la práctica, los circuitos de los contadores asincrónicos son mucho más simples que los circuitos de los contadores síncronos. La principal ventaja de los contadores síncronos es que pueden operar a frecuencias más altas.
b) Clasificación para el modo de contaje
Los contadores pueden ser progresivos o aumentar cuando cuentan en una secuencia de números crecientes, es sea, de los valores más bajos a los más altos como (1, 2, 3,4...). Estos contadores son también conocidos por el término inglés UP COUNTERS.
Los contadores pueden ser REGRESIVOS o DECRECIENTES cuando el contaje se hace de los valores más altos al más bajo como (4,3, 2, 1...). Estos contadores también son conocidos por el término inglés DOWN COUNTERS.
Aunque podemos hacer contadores usando funciones lógicas comunes e incluso flip-flops discretos, podemos confiar en práctica con varios circuitos integrados, ambos en la lógica TTL como CMOS, que ya tienen contadores completos puestos en ejecución.
Algunos circuitos tienen contadores con varias etapas facilitando, así, la implantación de proyectos digitales que hacen el contaje de gran cantidad de pulsos.
El uso de tales circuitos, no sólo facilita el proyecto, pero también reduce su coste, y los hace más confiables por el número más pequeño de piezas usadas.
A continuación, analizaremos el funcionamiento de los principales tipos de contadores con los que podemos contar para el proyecto de circuitos lógicos digitales tanto en TTL como en CMOS.
9.2 – Contadores asincrónicos
Como explicamos, en este tipo de contador, la señal del clock se aplica sólo a la primera etapa, permaneciendo sincronizada por las etapas anteriores.
En la figura 35 tenemos la estructura básica de un contador de este tipo utilizando flip-flops del tipo J-K.
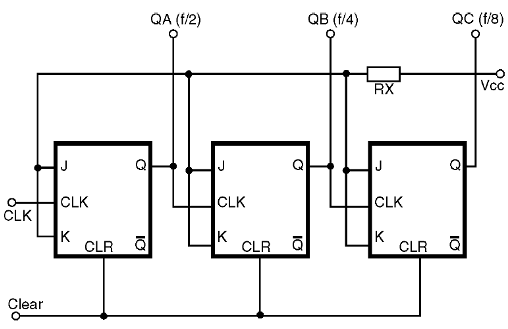
Utilizamos tres etapas o tres flip-flops conectados de tal manera que la salida Q de la primera es clock para el segundo, y la salida de Q de la segunda sirve como un clock para el tercero, y así sucesivamente, tantos como los bits que se necesitan para representar el número de contado.
Sabemos por lecciones anteriores que los flip-flops conectados en la forma indicada funcionan como divisores de frecuencia. Así, la señal del clock aplicada al primero tiene su frecuencia dividida por 2. La frecuencia será dividida por 4 en la segunda salida, y por 8 en la tercera salida.
Todo esto puede ser mejor visualizado por el diagrama de tiempo mostrado en la figura 36.
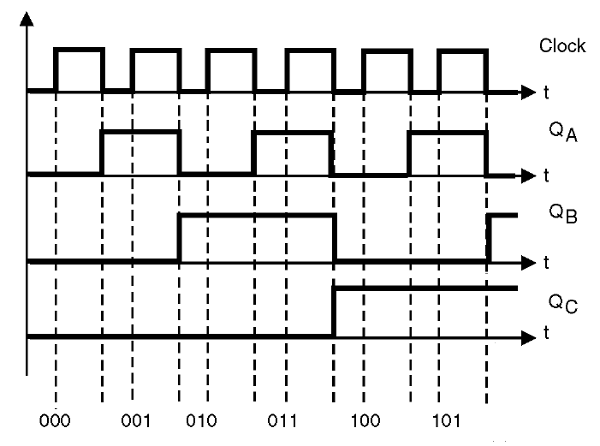
Pero si elaboramos una tabla verdadera con los niveles lógicos obtenidos en la salida de cada uno de los flip-flop, a cada pulso del clock aplicado, desde el instante en que todas las salidas son cero, tendremos algo interesante a considerar:
| ENTRADA | QC | QB | QA |
| 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 2 | 0 | 1 | 0 |
| 3 | 0 | 1 | 1 |
| 4 | 1 | 0 | 0 |
| 5 | 1 | 0 | 1 |
| 6 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 |
Vea que la secuencia de valores obtenidos 000, 001, 010, 011, 100, 101, 110 y 111 corresponde precisamente al contaje, en binario, de los pulsos de ¡0 a 7!
En otras palabras, este circuito cuenta los impulsos de entrada y proporciona salidas que corresponden a la representación binaria de este contaje.
Vea también que él hace el contaje que aumenta, es sea de 0 hasta 7.
También es fácil darse cuenta de que si cuando alcanzamos el séptimo impulso de entrada, cuando los flip-flops son 111 en sus salidas, recibiendo el octavo pulso todos los flip-flops cera, pasando las salidas a 000 y comenzando de nuevo el contaje.
Si, en lugar de 3 flip-flops, usamos cuatro, en el circuito que se muestra en la figura 37, tendremos el contaje de 0000 a 1111, o sea, un contaje cada vez mayor de 0 a 15 pulsos.
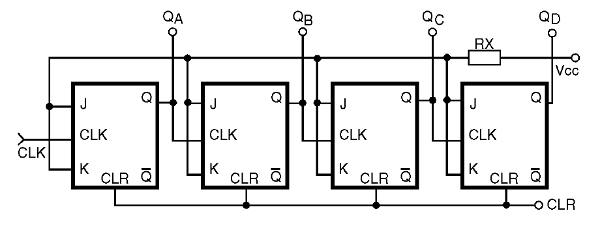
Ocho de estos flip-flop conectados en serie pueden contar hasta 256 pulsos y, con eso, proporciona una salida de 8 bits o 1 byte.
Por supuesto, necesitaremos tantos flip-flop como los bits necesarios para representar el número más grande que deseamos contar.
El circuito visualizado cambia la transición negativa de la señal del clock.
Supongamos ahora que, en lugar de utilizar como salidas de contaje las salidas Q de cada flip-flop, usamos las salidas complementares /Q como se muestra en la figura 38.
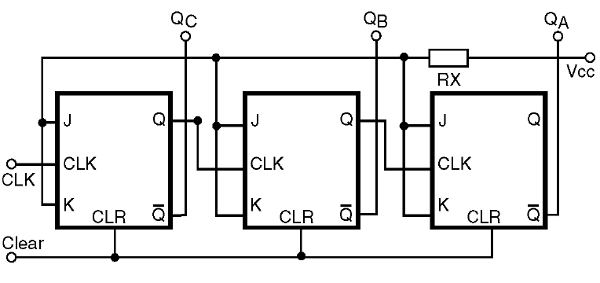
Es fácil ver que, a partir de la situación en la que todos los flip-flops estén reseteados el valor inicial correspondiente será de 000 o el valor binario 7, y la tabla verdadera obtenida tendrá en la salida los complementos de la tabla anterior. Esta tabla será dada por:
| ENTRADA | QC | QB | QA | VALOR BINÁRIO |
| 0 | 1 | 1 | 1 | 7 |
| 1 | 1 | 1 | 0 | 6 |
| 2 | 1 | 0 | 1 | 5 |
| 3 | 1 | 0 | 0 | 4 |
| 4 | 0 | 1 | 1 | 3 |
| 5 | 0 | 1 | 0 | 2 |
| 6 | 0 | 0 | 1 | 1 |
| 7 | 0 | 0 | - | 0 |
Este contador proporciona en sus valores binarios de salida que corresponden a la cuenta regresiva de los impulsos de entrada, a partir de 7. Esto es por lo tanto un contador descendente o DOWN COUNTER.
Como en el caso anterior, si tenemos más flip-flops podemos contar desde valores más altos. Con 4 flip-flops podemos partir el contaje de 15 y con 8 flip-flop de 255.
Vea que la cantidad máxima con la que podemos contar, con un contador de este tipo, depende únicamente de la cantidad de flip-flops utilizados.
Este valor puede calcularse mediante la fórmula:
n = 2x
Donde n es el valor máximo del contaje
x es el número de etapas o flip-flops utilizados
Para x = 4, por ejemplo, vamos a tener:
n = 24
n = 2 x 2 x 2 x 2
n = 16
Esto significa que a partir de cero podemos contar hasta 15, como hemos visto en los ejemplos de datos.
Para x = 8 tenemos:
n = 28
n = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2
n = 256
Un problema que ocurre con este tipo de flip-flop es que, cada flip-flop necesita un cierto tiempo para cambiar de estado. Esto significa que a medida que usamos más flip-flops en secuencia en un contador, los tiempos de cambio de estado suman y el conjunto necesita más tiempo para alcanzar el estado final deseado.
Si aplicamos un nuevo pulso de clock para contar a la entrada del circuito, antes de que el cambio de estado de todos los flip-flops del sistema ocurra, una operación errática puede ocurrir.
Así, la frecuencia máxima operativa de un contador se da por el tiempo requerido para que cada etapa cambie el estado multiplicado por el número de etapas utilizadas en el contador.
Por supuesto, en un mostrador con muchas etapas, el tiempo total puede limitar significativamente el rendimiento esperado.
9.3 – Contaje programada
Como hemos visto, los ciclos de contaje del ciclo dados como ejemplos en el ítem anterior son siempre alimentación de 2, o sea, son circuitos que cuentan hasta 2, 4, 8, 16, 32, etc.
¿Qué debemos hacer si necesitamos un circuito que tenga un ciclo de contaje diferente al de estos valores, o sea, que no sea una alimentación de 2?
Esto se puede hacer si tomamos en cuenta dos factores:
* Podemos utilizar la entrada CLEAR para restablecer la cuenta regresiva (ponerlo a cero) cuando alcanza el valor deseado. Por ejemplo, podemos reiniciar el contaje después de 5, o sea, en el 6, si queremos un contador que cuente de 0 a 5, o sea, que tenga 6 estados de salida, como se muestra en la tabla de verdad que se indica a continuación:
| ENTRADA | QC | QB | QA | |
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | |
| 6 | 0 | 0 | 0 | Estado Inestable |
En el sexto pulso, que corresponde al estado, 110 el circuito va a un estado que activa la entrada CLEAR y toma todos los flip-flops para ser reseteado.
Para este circuito la solución es simple. Vea que la situación en la que debemos tener la parte posterior a cero del contaje y por lo tanto la activación de la línea de CLR (clear) ocurre con una sola combinación de señales: QA y QB en el nivel alto.
Si usamos flip-flops que tienen entradas CLEAR activadas por el nivel alto, simplemente añada al circuito una entrada y un puerta con las entradas conectadas a las salidas QB y QC del contador, y la salida en la línea CLEAR común de todos los flip-flop, como se muestra en la figura 39.
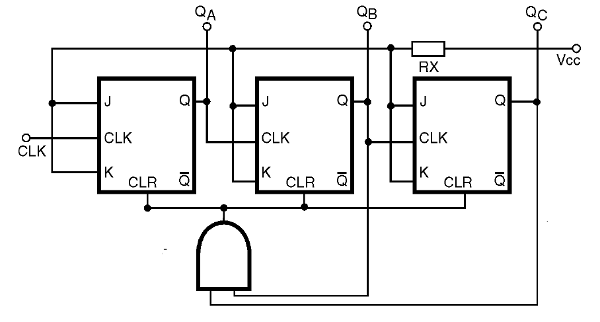
Si los flip-flops usados tienen un CLEAR activado en el nivel bajo, tal como el 7476 (TTL), apenas utilice una puerta NAND en vez de AND.
Si quisiéramos un contador hasta 4, por ejemplo, el estado en el cual ocurriría la activación de la entrada CLEAR ocurriría con la quinta combinación de salidas, o sea 101, que significa QC = 1 y QA = 1. Sería suficiente entonces conectar las entradas y las puertas a estas salidas, como se muestra en la figura 40.
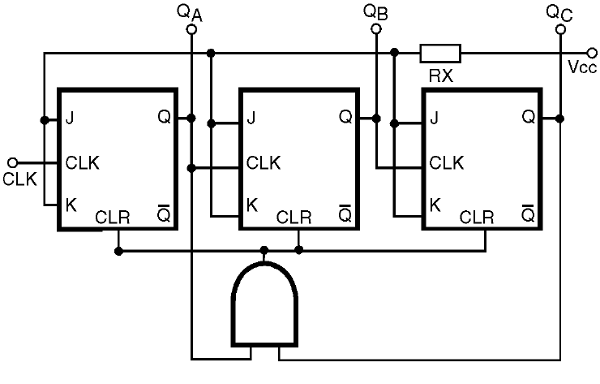
Un diagrama de tiempo puede mostrar al lector exactamente lo que sucede con el contador elaborado de esta manera. Este diagrama se muestra en la figura 41.
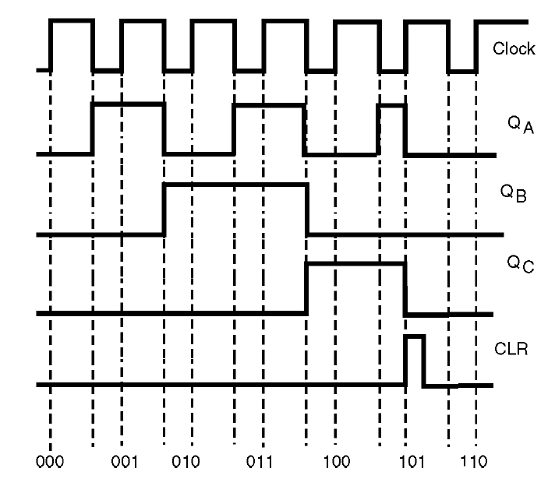
Tenga en cuenta que cuando las salidas alcanzan el estado 110, que sería el contaje del quinto pulso en el circuito, como se muestra en la figura 42, se produce un pulso de reajuste de corta duración. Esta corta duración se da precisamente en el momento en que los flip-flops conducen al cambio de estado, ya que "realimentan" las entradas del puerta AND.
En los ejemplos datos, hicimos la programación de contaje usando las entradas CLEAR de cada flip-flop.
Otra manera de proyectar un contador es utilizar las entradas PRESET en lugar de CLEAR. Para ello, nos aseguramos de que, en el momento en que se produzca el recuento del valor inmediatamente anterior al de la vuelta a cero, o sea, n-1, en lugar de tener los flip-flops cambiados, tenemos la activación de las entradas PRESET. De esta manera, en el siguiente pulso de clock (n) tendremos el contador de reset de nuevo a cero.
Para un contador de 6 estados, que después del quinto pulso resetea, tendremos la siguiente tabla verdad.
| Pulsos | QC | QB | QA | |
| 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | |
| 2 | 0 | 1 | 0 | |
| 3 | 0 | 1 | 1 | |
| 4 | 1 | 0 | 0 | |
| 5 | 1 | 0 | 1 | o Preset ‚ ativado |
| X | X | X | X | vuelve a zero en la transición del clock |
| 6 | 0 | 0 | 0 | |
| 7 | 0 | 0 | 1 | |
| 8 | 0 | 1 | 0 | |
| ETC. |
Un circuito que utiliza una puerta AND se muestra en la figura 43.
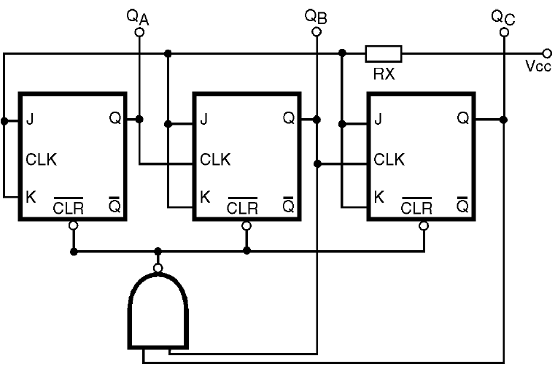
Vea que la detección de la condición de producción del pulso prefijado debe ser reconocida con los niveles 101 en las salidas de las platinas de contadores, y con el pulso yendo al alto nivel en la entrada de contaje.
Para obtener la configuración 1111, lo que nos permitiría utilizar una de cuatro entradas y el puerta, sólo tiene la salida/QB en lugar de QB.
Por lo tanto, sólo tiene que utilizar el puerta y conectarlo en las flip-flops PRESET (PR) entradas.
Si las entradas se activan en el nivel bajo (/PR) sólo tiene que intercambiar el puerta y con un puerta NAND de cuatro entradas.
9.4 – Contadores Up/DFown (Progresistas Y Regresivos)
Usando algunos artificios, por ejemplo, los puertas lógicos apropiados, podemos programar un contador para que ambos puedan contar progresivamente como regresivo.
Estos artificios se encuentran ya incrustados en algunos circuitos integrados que pueden ser utilizados para el contaje progresivo como regresivo, dependiendo únicamente de la programación realizada por un pino externo.
Usando 3 etapas, por ejemplo, podemos tener un contador arriba/abajo como se muestra en la figura 44.
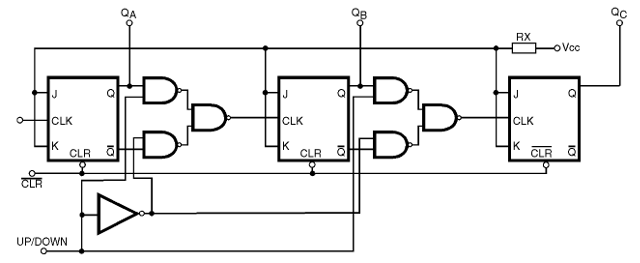
Se puede usar una entrada (UP/DOWN) para determinar la dirección del contaje. Se trata de una entrada de selector de datos, que se puede utilizar para cambiar el modo de funcionamiento de las etapas de este circuito.
El funcionamiento de este circuito es fácil de explicar. Como hemos visto en esta lección, si usamos las salidas Q de los flip-flop de un contador, el contaje va a aumentar, pero si usamos las salidas/q el contaje está disminuyendo.
Por lo tanto, lo que hacemos es poner un circuito selector en estas salidas, por lo que pone la salida Q de cada flip-flop en la entrada del clock de la siguiente cuando el contaje debe ser progresivo, pero pone la salida /Q en la entrada de la siguiente cuando el contaje debe ser decreciente. Tres puertas NAND para cada etapa pueden hacer esto desde la señal de comando UP/DOWN.
9.5 – Contadores síncronos
Sincronizar el contaje por un solo clock, aplicado a todas las etapas, no es sólo una necesidad de los circuitos más complejos, sino también el Me involucro Lógica más elaborada, principalmente las utilizadas en informática, automatización e instrumentación. La sincronización de todas las etapas por el mismo clock también tiene ventajas operacionales importantes.
Como hemos visto, en los contadores asincrónicos, los tiempos de conmutación de cada flip-flop influyen en el funcionamiento final del circuito, ya que son acumulativos. En otras palabras, cada etapa debe esperar a que el anterior complete la operación antes de que comience.
Usando la lógica sincronizada, o sea, un contador en el que todas las etapas están sincronizadas por un solo clock, este problema no existe y podemos tener contadores mucho más rápidos, de hecho contadores cuya velocidad es independiente del número de pasos.
Para mostrar cómo se puede hacer esto tomaremos como ejemplo el circuito de la figura 45.
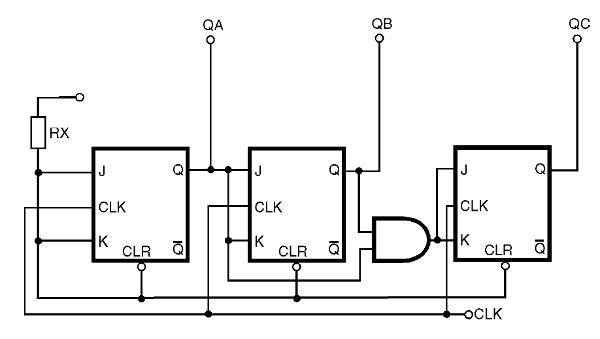
Este circuito utiliza el tipo flip-flops de J-K conectados de una manera llamada PARALLEL CARRY.
El término "Carry" se refiere a "va uno" o "lleva" y es ampliamente utilizado, siendo guardado el original en inglés en la mayor parte de la documentación electrónica digital en Español.
En esta forma de conexión, J y K del primer flip-flop se mantienen en el nivel alto con la ayuda de una resistor conectada al positivo de la alimentación (Vcc). De esta manera, el primer flip-flop cambia de estado a cada pulso de clock.
Sin embargo, J del segundo flip-flop está conectado a la salida Q de la primera. Esto significa que el segundo flip-flop sólo cambiará de estado cuando el primer flip-flop es reseteado, o sea, cada dos pulsos de clock.
Del mismo modo, con el uso de un puerta y el tercer flip-flop sólo cambiará de estado cuando las Q salidas del primer y segundo flip-flop están en el nivel 1, o sea, cada 4 pulsos de clock.
Para 4 bits, usando 4 etapas, podemos utilizar el circuito demostrado en la figura 46.
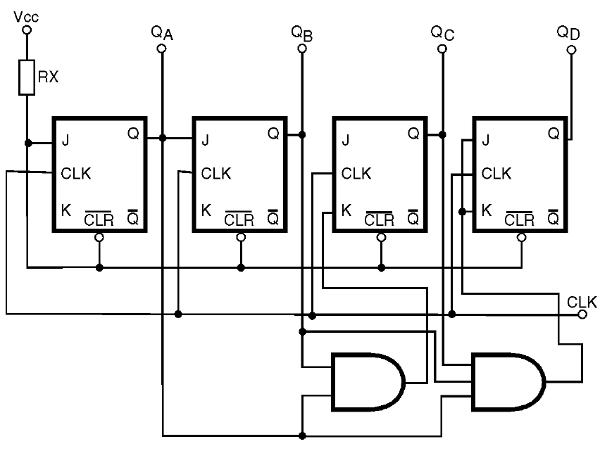
Un problema que se produce con este tipo de configuración es que, de 3 etapas, a cada etapa que hemos añadido en el contador, debemos poner un adicional y el puerta, cuyo número de entradas se incrementará. Tan para 4 etapas el puerta debe tener tres entradas, para 5 etapas el puerta debe tener 4 entradas y así sucesivamente.
Una forma de evitar este problema es utilizar un ajuste de contador diferente que se muestra en la figura 47 y que se llama RIPPLE CARRY.
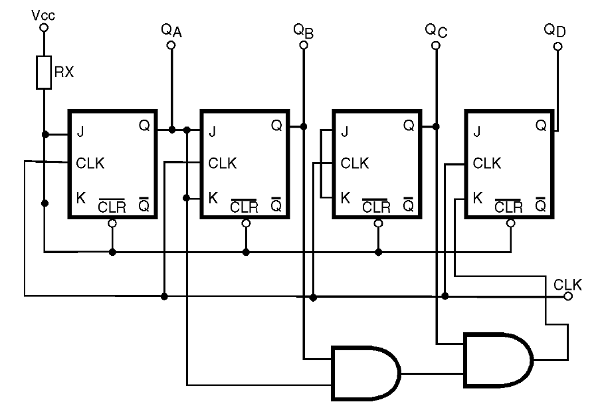
Le recordamos que la palabra " ripple" significa ondulación o variación, y también se mantiene en la forma original cuando trabajamos con electrónica digital.
En este circuito los puertas utilizados siempre necesitan tener sólo dos entradas, lo cual es importante para la implementación práctica del contador. Sin embargo, como desventaja de este circuito tenemos una limitación de la velocidad de operación, porque como la señal para cada etapa viene de la puerta anterior tenemos que considerar su demora.
9.6 – Contadores síncronos programables
De la misma manera que en el caso de los contadores asincrónicos, también es necesario, en ciertas aplicaciones, contar con valores que no sean potencias de 2.
La división o contar por otros valores se puede hacer con la ayuda de los puertas que están conectados para "sentir" cuando un cierto valor es alcanzado y después reseteando todos los flip-flop.
La técnica es exactamente la misma que vimos en el caso de los contadores asincrónicos, utilizando puertas y otras funciones lógicas más sencillas.
También es importante saber que hay circuitos integrados, tanto de las familias TTL como de las subfamilias como CMOS que ya contiene recursos para contar hasta valores que no sean potencias de 2 o así que se pueden utilizar en esta función con pocos puertas externos.
Más tarde, cuando damos circuitos prácticos con flip-flops TTL y CMOS tendremos varios tipos de divisores utilizando circuitos integrados comunes.
9.7 – Contadores TTL
Utilizando los puertas lógicos y los flip-flop, podemos implementar contadores que contengan hasta cualquier valor, o dividir una señal de entrada por cualquier número entero. Sin embargo, en la práctica podemos contar con muchos circuitos integrados en la tecnología TTL que ya contienen estos circuitos completos en un único chip, e incluso con recursos que permiten cambiar su funcionamiento con el fin de obtener el contaje a un valor determinado previamente programado.
El uso de estos circuitos, que se pueden conectar juntos (en cascada), permite contar hasta prácticamente cualquier valor entero con un mínimo de componentes externos y alcanzar velocidades bastante altas.
A continuación, veremos algunos de los principales contadores de circuitos integrados en la tecnología TTL.
Estos contadores pueden ser obtenidos tanto en la familia Standard como en sus diferentes subfamilias.
7490- Contador de Década
El circuito integrado 7490 es uno de los contadores TTL más populares, conteniendo en su interior cuatro flip-flops ya interconectados para funcionar como divisores por 2 y 5. Esto significa que estos divisores pueden ser utilizados para tener un contador hasta 2 y un contador hasta 5, y juntos, como un contador hasta 10.
En la figura 48 tenemos la disposición de los terminales de este circuito integrado.
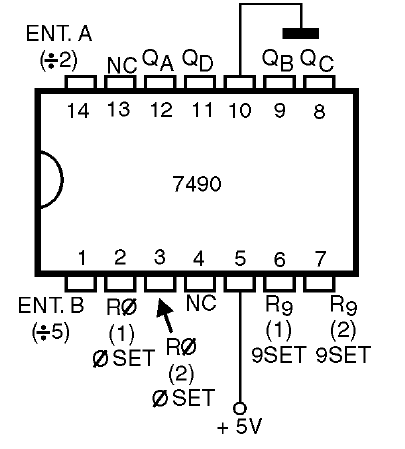
El circuito integrado 7490 se puede utilizar de tres maneras diferentes, siempre con las entradas R0(1), R0(2), R9(1) y R9(2) puesta a la tierra:
* Cuando conectamos la entrada B a la salida de QA y aplicamos la señal del clock a la entrada a, el circuito funciona como un contador BCD, esto es, cuenta hasta 10, con las salidas decimales codificadas en binarias presentadas en los pinos QA, QB, QC y QD. Este enlace se muestra en la figura 49.
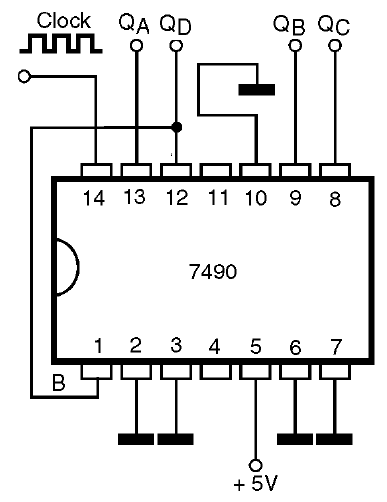
La tabla verdad para los pulsos aplicados en la entrada en este modo de operación será:
| Pulso | QD | QC | QB | QA |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 |
Tenga en cuenta que la salida de QA es el peso más bajo (2) y la salida QD es el peso más alto (8).
* Cuando conectamos la salida QD a la entrada a y aplicamos la señal del clock a la entrada B, tendremos el circuito funcionando como un divisor de frecuencias por 10 simétricos. Tendremos una señal cuadrada en la salida AQ (ciclo activo de 50%) con 1/10 de la frecuencia del clock. Este modo de operación tiene los enlaces mostrados en la figura 50.
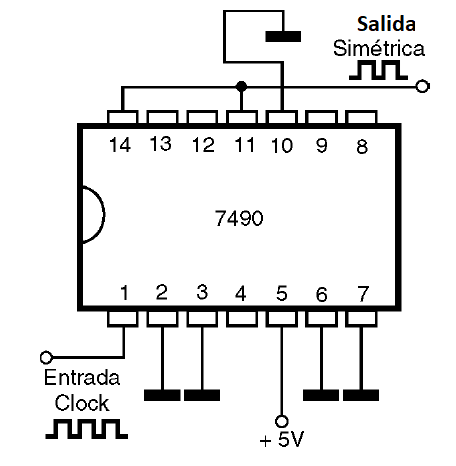
* Por último, cuando queremos utilizar el circuito como divisor por 2 o 5, con sectores independientes, no hay necesidad de conexión externa alguna.
La señal aplicada en CLK1 tiene la frecuencia dividida por 2, y la señal aplicada en el CLK2 tiene la frecuencia dividida por 5. En el funcionamiento normal, las entradas R0(1) y R0(2) deben mantenerse en un nivel bajo.
Para la serie normal o standard la frecuencia máxima de clock es de 18 MHz, y cada circuito integrado consume una corriente media de 32 mA.
Para reiniciar la cuenta regresiva, simplemente tome las entradas 0 SET al nivel alto por un instante.
Como el contador es de tipo "ripple, cambiado de estado con la frente negativa de la señal del clock, es necesario que la señal utilizada para su excitación esté libre de cualquier repique.
7492 – Contador-Divisor para 12
Este circuito integrado contiene cuatro flip-flops conectados como un divisor por 2, y un divisor por 6. Los dos divisores se pueden utilizar independientemente. El pinaje de este circuito TTL integrado se muestra en la figura 51.
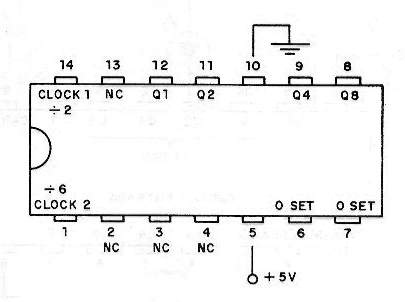
El disparador de flip-flops ocurre en la transición de la señal de clock de nivel alto para el nivel bajo (frente negativa de la señal de entrada). Para resetear el contador a 0000, simplemente aplique el nivel lógico 1 en las entradas de 0 SET.
Hay tres modos de operación para este circuito integrado:
* Como contador hasta 12, simplemente conecte la salida de QA a la entrada B. la señal del clock se aplica a la entrada A. La tabla verdad para este modo de operación será:
| ENTRADA | QD | QC | QB | QA |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 0 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 1 | 0 | 1 | 0 |
| 11 | 1 | 0 | 1 | 1 |
En el décimo segundo pulso, el circuito resetea y vuelve a la salida 0000.
En la segunda forma de operación conectamos la salida QD a la entrada A. El circuito funcionará como un divisor de frecuencia simétrico. La frecuencia de la señal de clock aplicada a la entrada B se dividirá por 12 y la señal tendrá un ciclo activo de 50%.
En la operación sin ninguna conexión externa, la señal aplicada a la entrada Atendrá su frecuencia dividida por 2 y la señal aplicada en la entrada B tendrá su frecuencia dividida por 6.
La frecuencia de funcionamiento máxima del 7492 de la serie normal (standard) es 18 MHz y el consumo por CI es de la orden de 31 mA.
7493 - CONTADOR BINARIO DE 4 BITS
En este circuito integrado encontramos 4 flip-flops que forman un divisor por 2 y un divisor por 8. Juntos, pueden dividir o contar hasta 16, proporcionando una salida completa de 4 bits.
En la figura 52 tenemos el pinaje de este circuito integrado.
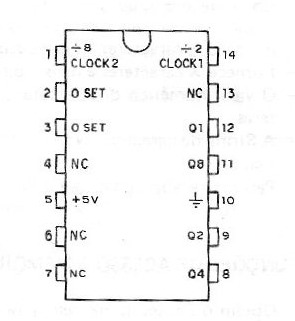
En funcionamiento normal las entradas 0 SET (2) y SET (3) se mantienen a bajo nivel y el disparo ocurre con la transición de la señal de clock de alto nivel al nivel bajo.
La operación puede ocurrir en dos modos:
Con la salida Q1 conectada a la entrada 14 y la señal de entrada aplicada en la entrada 1 el circuito cuenta en la secuencia normal de 0000 a 1111 y en las salidas Q1, Q2, Q3 y Q4 tendremos los valores correspondientes.
Sin conexiones externas, podemos utilizar el circuito como divisor por 2 y 8 independientes, aplicando las señales en las entradas A y B respectivamente.
74190 – Contador/divisor para 10 Up/Down
Esta es la versión de 74190 que cuenta en un sentido progresivo y regresivo. El pino de este circuito integrado se muestra en la figura 53.
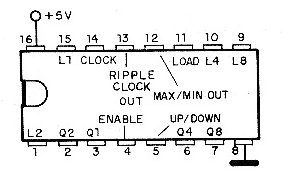
En el funcionamiento progresivo normal, la entrada LOAD (carga) debe mantenerse en el nivel alto, la habilitación (EN) en el nivel bajo, y la entrada UP/DOWN debe mantenerse en el nivel bajo. Con esta entrada en el nivel alto él cuenta regresivamente.
El contador avanza una unidad en el contaje en la transición de bajo nivel al alto nivel del pulso del clock.
La frecuencia de contaje máxima para la versión standard es de 20 MHz y el consumo medio por circuito integrado es de 65 mA.
9.8 – Contadores/divisores CMOS
También podemos contar con varios circuitos integrados en la tecnología CMOS que contienen contadores y divisores. A continuación veremos algunos de los más importantes.
4017 – Contador/divisor para 10
Este circuito integrado contiene un conjunto de flip-flops y un sistema decodificador para las salidas que proporcionan señales de tipo 1 de octubre.
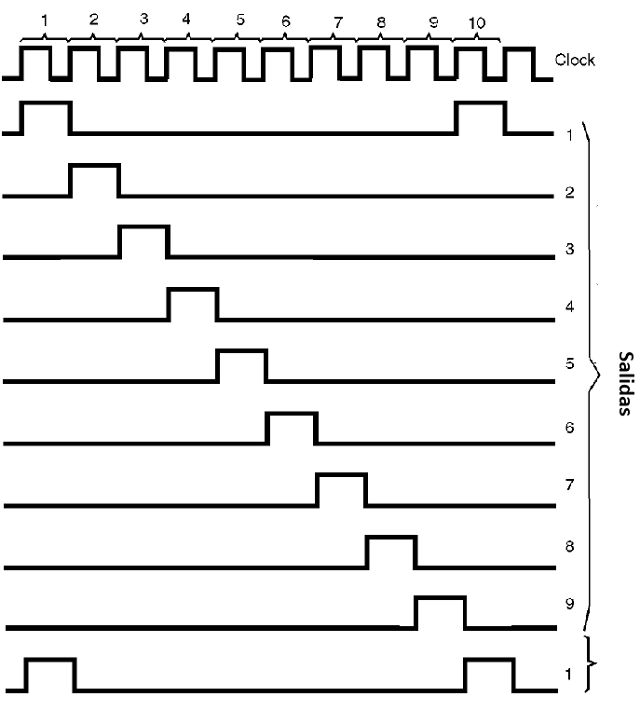
En este tipo de salida, en cada pulso sólo una salida va al nivel alto, devolviendo el anterior al nivel bajo. Así, para 10 impulsos de entrada, las salidas pasan secuencialmente al nivel alto.
En la figura 54 tenemos el pinaje de este circuito integrado.
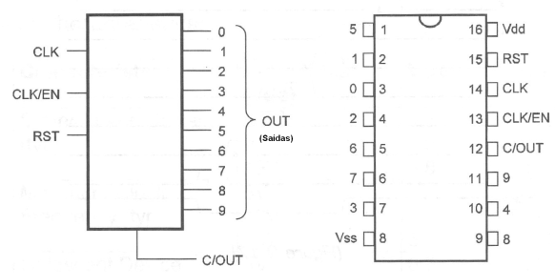
En el funcionamiento normal, contando hasta 10, las entradas RST y EN se deben mantener a un nivel bajo. Tomando la primera entrada RST al nivel alto el contador es reseteado. Si la entrada EN fuera llevada al nivel alto, el contaje queda paralizado.
En la figura 55 tenemos las formas de onda de este contador, mostrando cómo en cada instante siempre tenemos sólo una salida en el nivel alto.
Al igual que con todos los circuitos CMOS, la frecuencia de contaje máxima depende de la tensión de alimentación. La tabla abajo proporciona las características de este IC:
|
Característica |
Condiciones (VDD) |
Valor |
|
Corriente de salida drenada/suministrada tip. |
5 V 10 V 15 V |
0,88 mA 2,25 mA 8,8 mA |
|
Frecuencia máxima de clock (tip) |
5 V 10 V 15 V |
2 MHz 5 MHz 6 MHz |
|
Corriente reposo máxima |
5 V 10 V 15 V |
0,3 mA 0,5 mA 1,0 mA |
|
Banda de tensiones de la alimentación |
3 V a 15 V |
4018- Contador/Divisor Por N
Este circuito integrado puede hacer que la división o el contaje de pulsos en valores de hasta 10 programado por las conexiones externas.
Su pinaje se muestra en la figura 56.
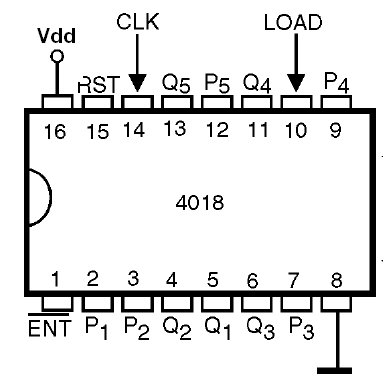
Su operación se detallará en el siguiente capítulo como la base de los contadores más complejos.
Sus principales características se dan en la siguiente tabla:
|
Característica |
Condiciones (Vdd) |
Valor |
|
Corriente drenada/suministrada (tip) |
5 V 10 V 15 V |
0,88 mA 2,25 mA 8,8 mA |
|
Frecuencia máxima del clock |
5 V 10 V 15 V |
4 MHz 9 MHz 14 MHz |
|
Corriente reposo máxima |
5 V 10 V 15 V |
0,3 mA 0,5 mA 1,0 mA |
|
Banda de tensiones de la alimentación |
3 V a 15 V |
Sumário
Curso de Electrónica - Electrónica Digital (CUR5000)
Curso de Electrónica - Electrónica Digital – Parte 1 (CUR5001S)
Curso de Electrónica Digital – Parte 2 - El Álgebra de Boole (CUR5002S)
Curso de Electrónica - Electrónica Digital - Parte 6 - Los Elementos Biestables (CUR5006S)
Curso de Electrónica - Electrónica Digital - Parte 9 - Contadores Digitales (CUR6002S)
Curso de Electrónica - Electrónica Digital - Parte 13 - Memorias, ADCs y DACs (CUR6006S)




