5.1 - Las tablas verdad
Las distintas señales de entrada aplicadas a una función lógica, con todas sus combinaciones posibles, y la salida correspondiente, se pueden colocar en una tabla. Ya hemos tenido un sentido de eso en las primeras lecciones.
En las columnas de entrada ponemos todas las combinaciones posibles de niveles lógicos que las entradas pueden tomar. En la columna correspondiente a la salida ponemos los valores que esta salida asume de acuerdo con los niveles lógicos correspondientes en la entrada.
Esta tabla, como ya hemos visto, se llama "tabla verdad" o " truth table" Si adoptamos el término en inglés.
De esta manera, estudiamos que la tabla verdad para una función AND de dos entradas será representada como se muestra en la figura 121.
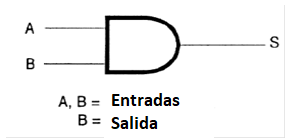
| A | B | S |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Vea que en las columnas de entrada (A y B), para tener todas las combinaciones posibles, hacemos el equivalente de un conteo binario de 0 a 3, ya que:
00 = 0
01 = 1
10 = 2
11 = 3
Para una tabla verdad hecha para una puerta AND de 3 entradas tendremos:
| A | B | C | S |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
En este caso, las combinaciones de niveles lógicos en la entrada corresponden realmente a un conteo binario de 0 a 7 ya que:
000 = 0
001 = 1
010 = 2
011 = 3
100 = 4
101 = 5
110 = 6
111 = 7
Note entonces que para una función de 2 entradas, tenemos 4 posibles combinaciones de señales de entrada. Para una función de 3 entradas, tendremos 8 combinaciones y para una función de 4 entradas, 16 combinaciones y así sucesivamente.
El conocimiento de la contaje binario facilita enormemente la elaboración de tablas verdad cuando se deben analizar todas las combinaciones posibles de niveles lógicos en 2, 3 o 4 entradas.
Así, una vez que el lector conozca el comportamiento de las funciones principales, sabiendo lo que ocurre en la salida de cada uno, cuando tenemos ciertas entradas y saber cómo elaborar tablas verdad, es fácil combinar funciones y saber lo que sucede en sus salidas.
De hecho, el punto principal de la información técnica de los circuitos de la lógica digital es su tabla verdad.
Además, debemos tener en cuenta que, además de las combinaciones de los niveles lógicos de las entradas, también podemos encontrar columnas que tengan en cuenta los niveles lógicos de entradas especiales como una entrada de habilitación (EN), una entrada que lleva el dispositivo a un tercer Estado o incluso causar una transición desde el nivel de la señal.
En este caso, como hemos visto, independientemente de lo que ocurra en las entradas, la salida estará en un estado de alta impedancia. Las tablas verdad pueden incluir este tercer estado del dispositivo.
5.2 - Lógica Combinacional
Llamamos "lógica combinacional" la lógica que rige el funcionamiento de varias funciones más sencillas cuando se combinan, o se montan en un circuito más complejo.
Para entender cómo funciona, empecemos por un simple ejemplo de lógica combinada usando tabla verdad para saber, por ejemplo, lo que sucede en su salida, con el circuito de la figura 122.
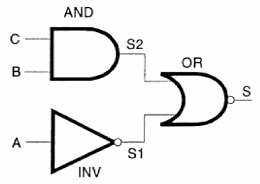
Este circuito hace uso de una puerta AND, un inversor y una puerta OR. El resultado de esta configuración es una función combinada que tiene tres entradas y una salida.
Para elaborar la tabla verdad para este circuito, y así determinar todas las salidas posibles en función de las entradas, debemos tener en cuenta que está formada por dos etapas.
En el primer paso tenemos la puerta AND y el inversor, mientras que en el segundo paso tenemos la puerta OR. Esto significa que las salidas de los circuitos del primer paso, que llamamos S1 y S2, son las entradas del segundo paso.
Tenemos que tener en cuenta estos resultados en la elaboración de la tabla verdad que tendrá en su parte superior las siguientes variables:
| A | B | C | S1 | S2 | S |
A, B y C son las entradas de circuitos. S1 y S2 son puntos intermedios del circuito, o salidas intermedias, que necesitan ser analizadas para obtener S que es la salida final del circuito.
Empezamos por poner en A, B y C todas sus condiciones posibles, o todas las combinaciones de niveles lógicos que se pueden aplicar al circuito:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | |||
| 0 | 0 | 1 | |||
| 0 | 1 | 0 | |||
| 0 | 1 | 1 | |||
| 1 | 0 | 0 | |||
| 1 | 0 | 1 | |||
| 1 | 1 | 0 | |||
| 1 | 1 | 1 |
Vea que como tenemos 3 entradas, las posibles combinaciones para los niveles de entrada lógico son 8. Los niveles aplicados son por lo tanto equivalentes al conteo binario de 0 a 7.
El siguiente paso es colocar los valores posibles de S1 que corresponden a la salida del inversor. Sabemos que la tabla verdad para el inversor es:
A S
0 1
1 0
Ahora, como en nuestro caso A es la entrada del inversor, y S1 es su salida, podemos dejar para la determinación de toda la columna S1 simplemente revirtiendo los valores de la columna A, de la siguiente manera:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | 1 | ||
| 0 | 0 | 1 | 1 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 1 | 1 | 1 | ||
| 1 | 0 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | ||
| 1 | 1 | 0 | 0 | ||
| 1 | 1 | 1 | 0 |
Para encontrar los valores de la columna S2, observamos que corresponde a la tabla verdad de la y la función AND, donde las entradas correspondientes son B y C y la salida es S2. Por lo tanto, aplicamos la y la función de las entradas B y C, colocando los resultados en la columna S2.
B - C - S2
0 - 0 - 0
0 - 1 - 0
1 - 0 - 0
1 - 1 - 1
Como tenemos dos entradas, los resultados obtenidos son 4, pero observamos que en la tabla principal, las cuatro combinaciones de entrada se repiten dos veces.
Tenemos entonces:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 1 | 0 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 0 | 1 |
Por último, teniendo en cuenta que S1 y S2 son entradas de un puerta o de dos entradas, cuya salida es S y tiene por tabla verdad la que se muestra a continuación, podemos elaborar la columna final de las salidas (S)
S1 - S2 - S
0 - 0 - 0
0 - 1 - 1
1 - 0 - 1
1 - 1 - 1
En este caso, también, la combinación de 4 entradas se repite dos veces.
La tabla final es entonces:
| A | B | C | S1 | S2 | S |
| 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
Es una función muy interesante que se puede definir como "la que proporciona un nivel alto sólo cuando la entrada A está en nivel bajo, sin importar las otras entradas o incluso cuando las tres entradas están en el nivel alto".
Por supuesto, no sabemos en qué aplicación práctica el lector puede necesitar tal función, pero es el ejemplo de cómo se puede obtener y cómo podemos predecir su funcionamiento para todas las entradas posibles, utilizando tablas verdad.
5.3 - Cómo Proyectar Un Circuito Combinacional
El problema de saber qué pasa con la salida de un circuito formado por muchas funciones lógicas, cuando sus entradas reciben varias combinaciones de señales, no es la más importante para el proyectista de equipos digitales.
De hecho, mucho más importante que este procedimiento es precisamente hacer lo contrario, es decir, proyectar un circuito que, dependiendo de ciertas señales de entrada, proporcione exactamente en la salida lo que se desea.
El proyecto de un circuito que tiene una determinada función implica un procedimiento de síntesis en pocos pasos.
En el primer paso se debe definir el problema, estableciendo exactamente cuál es la función a ejecutar, es decir, qué entradas y qué salidas.
Un segundo paso plantea el problema en una tabla verdad o en la forma de ecuaciones lógicas. El procedimiento que vamos a discutir en este curso es básicamente el de obtener las funciones de las tablas verdad y las ecuaciones lógicas.
Finalmente, en un tercer paso obtenemos el circuito que realiza las funciones deseadas.
En la tercera etapa, tenemos un punto importante a considerar que consiste en minimizar el circuito, ya que en la mayoría de los casos se puede implementar la misma función de muchas maneras diferentes como atestigua el simple circuito mostrado en la figura 123.
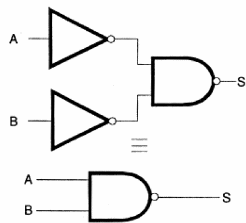
Vea que podemos tener el mismo circuito con diferentes cantidades de puertas, lo que significa que en la práctica uno debe tener en cuenta este hecho.
No es sólo el número de puertas que determinarán la configuración final, sino su coste y eventual uso en otras partes del circuito.
Por ejemplo, si el circuito ya está utilizando dos inversores de los seis disponibles en un circuito integrado y nuestra función tiene una solución un poco más grande, pero que utilizan estos inversores será interesante adoptarlo para aprovecharse de los inversores ociosos.
Otro punto a tener en cuenta es que hoy en día existen circuitos lógicos digitales que consisten en funciones en una determinada cantidad y que pueden ser interconectados mediante la programación.
Así, el mismo circuito, sólo necesita ser programado de una cierta manera para realizar las funciones deseadas, interconectando, a través de este programa las puertas que se utilizarán.
Lo siguiente dará un ejemplo de cómo podemos conseguir los circuitos de una tabla verdad.
Pedimos al lector que preste especial atención a estos procedimientos, los cuales, aunque simples, requieren atención porque consisten en una potente herramienta de trabajo para el proyectista de circuitos digitales.
Paso 1 - Determinación de las ecuaciones lógicas
Les recordamos que para las funciones estudiadas tenemos las siguientes representaciones:
* Función E (AND)
Y=A.B
* Función No-E (NAND)
Y=/(A.B)
* Función OU (OR)
Y=A+B
* Función No-OU (NOR)
Y=/(A+B)
* Función No (NOT) o inversor
Y=/A
* Función o exclusivo (Exclusive OR)
Y=A (+) B
Tomemos como ejemplo la tabla verdad abajo para determinar la función lógica correspondiente:
| A | B | C | Y | LÍNEA |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 2 |
| 0 | 1 | 0 | 1 | 3 |
| 0 | 1 | 1 | 0 | 4 |
| 1 | 0 | 0 | 0 | 5 |
| 1 | 0 | 1 | 1 | 6 |
| 1 | 1 | 0 | 1 | 7 |
| 1 | 1 | 1 | 0 | 8 |
En este ejemplo, A, B y C son las entradas e Y la salida.
Indicamos los números de las líneas en la última columna con el fin de facilitar las explicaciones que vamos a dar a continuación.
Como podemos ver, tenemos salidas en el nivel 0 para las filas 0, 3, 5 y 6 mientras que para las filas 1, 2. 4 y 7 tenemos la salida 1.
Esto significa que tendremos la función OU para las filas cuya salida es 1 puede ser vista como u operaciones con tablas que tendrían 1 en la salida sólo en las filas 1, 2, 4 y 7, como se muestra a continuación:
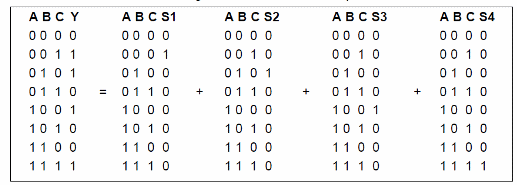
Esto nos permite escribir las ecuaciones lógicas para cada una de las cuatro tablas de la siguiente manera:
S1 = /A. /B. C que corresponde a = 0, B = 0, y C = 1
S2 = /A. B. C que corresponde a = 0, B = 1, y a = 0
S3 = /A. /B. C que corresponde a A = 1, B = 0, y C = 0
S4 = A. = 1 C que corresponde a = 1, B = 1 y C = 1
Como la salida S es la combinación de las cuatro funciones que tenemos:
S = S1 + S2 + S3 + S4
Reemplazando con los valores encontrados tenemos:
S = /A./B.C + /A.B.C + /A./B.C + A.B.C
Ésta es entonces la función lógica que representa la tabla verdad que propusimos como parte inicial del problema y para la cual debemos encontrar un circuito equivalente.
Paso 2 - Implantación de los Circuitos Combinacional
A medida que estudiamos en las lecciones anteriores, es posible utilizar los puertas NAND y NOR como bloques lógicos universales desde los que se puede elaborar cualquier otra función o incluso funciones más complejas.
Es por esta razón que los circuitos integrados que contienen estas funciones son los más comunes en todas las familias lógicas.
Para ejemplificar cómo se puede hacer esto, vamos a tomar como ejemplo una función un poco más simple que la que obtuvimos en el paso anterior.
Tomemos la expresión como un ejemplo:
S = A. B. /C + A. /B. /C
Podemos intentar implementarlo utilizando puertas NAND, y eventualmente inversores, ya que la barra sobre cada letra indica su negativo, como ya hemos estudiado.
La operación (.) se puede realizar utilizando una puerta NAND que está conectado a un inversor y proporciona una puerta AND.
Así, como se muestra en la figura 124 podemos implementar A.B.C usando una puerta NAND de 3 entradas y un inversor.
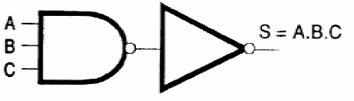
La operación A.B.C puede ser implementada como se muestra en la figura 125.
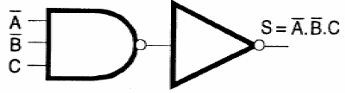
La suma (+) puede ser implementada con una puerta AND conectado a dos inversores como se muestra en la figura 126.
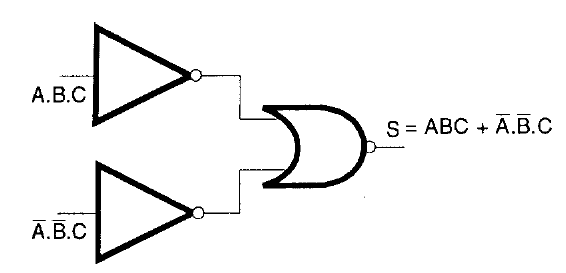
Combinando los tres circuitos podemos alcanzar la configuración final deseada, que se muestra en la figura 127.
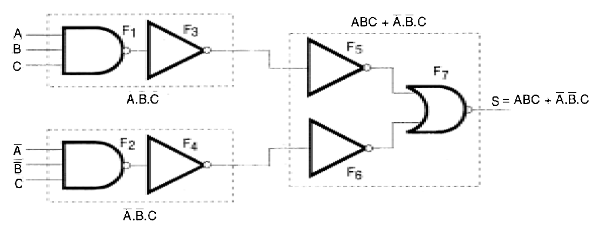
Vea que la inversión de la inversión utilizada en el circuito interior nos lleva al circuito original. Esto significa que podemos simplificar la configuración eliminando las reversiones dobles en serie.
Esto nos lleva a la configuración final del circuito que se muestra en la figura 128.
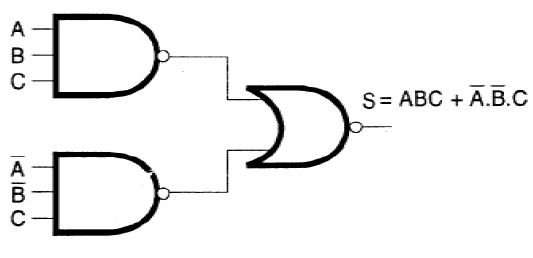
También vemos que cuando tenemos una expresión formada por la suma de productos, podemos utilizar puertas NAND sin necesidad de inversores, simplemente recordando dos propiedades:
Las combinaciones de entrada pueden ser aplicadas para puertas NAND.
Las salidas de las puertas NAND se pueden aplicar a la entrada de una segunda puerta NAND obteniendo la función deseada en la salida.
Ahora hagamos un intento de implementar una función usando puertas NOR, que serán elegidos cuando tengamos un producto de sumas.
Tomemos como ejemplo la función:
S = /(A + B + C) . /(A + B + C)
Las sumas pueden obtenerse fácilmente desde las puertas NOR con la salida aplicada a un inversor. La negación de NOR es OR. El circuito equivalente para tres entradas se muestra en la figura 129.
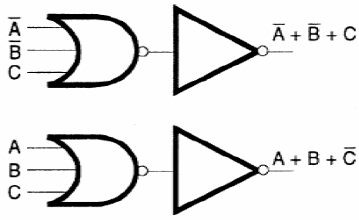
El producto de las dos sumas se obtiene con dos inversores, aplicando las señales a otro o puerta OR, o sea, la otra configuración OR.
Al igual que en las dos líneas de señal tenemos inversores en serie, y como el inverso de la inversa de un nivel lógico es en sí, podemos simplificar el circuito mediante la eliminación de todos los inversores.
Esto nos permite llegar a la configuración final que se muestra en la figura 130.
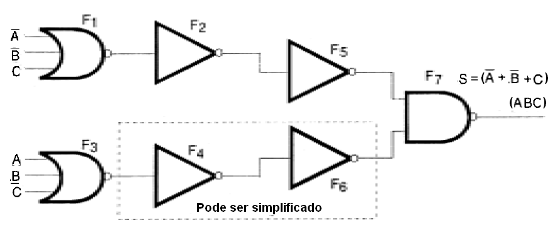
Así que si queremos implementar una función consistente en un producto de suma basta conseguir dos procedimientos básicos:
Aplicar las entradas correspondientes a cada suma a una o puerta que se pueda obtener asociando a un puerta OR a un inversor.
Aplicar las salidas obtenidas en las funciones que se deben multiplicar a los inversores que están conectados a las entradas de una puerta OR final o, también obtenidas con la asociación de un inversor a un puerta NOR.
Como los inversores seriales se cancelan, pueden ser eliminados y el circuito puede ser implementado usando solamente puertas NOR.
Vea al lector que podemos resolver el problema de la implantación de circuitos combinados, reduciendo las funciones a productos de sumas o incluso la suma de productos, casos en los que podemos trabajar con funciones NAND o NOR, como se muestra en la figura 131.
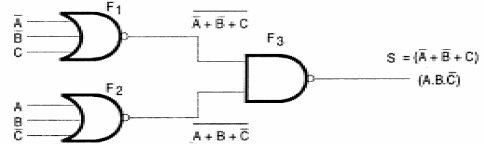
Como las dos soluciones conducen a los mismos resultados, en un proyecto práctico, es interesante analizar las configuraciones obtenidas para un problema en ambos casos. Se adopta entonces la solución que utiliza menos circuitos, o incluso más conveniente, por ejemplo, aprovechando los puertas ociosas de un circuito integrado ya utilizado en el mismo proyecto para otros fines.
Por supuesto, al utilizar las puertas contenidas en los circuitos integrados reales, el lector debe ser consciente de las características eléctricas, además de otras.
Lo que vimos, por lo tanto, es sólo un ejemplo de cómo podemos proceder a implementar funciones complejas utilizando los puertas.
El grado de complejidad de estas funciones puede aumentar enormemente, en cuyo caso el trabajo "manual" descrito se vuelve difícil. Existen softwares que ayudan a proyectar esos circuitos, que deben ser buscados para aquellos que deseen realizar este tipo de proyectos.
5.4 – Simplificando y Minimizando
Una consecuencia de la posibilidad de construir funciones complejas desde puertas básicos como OR y AND (OR y E), es capaz de optimizar un proyecto aprovechando pocos tipos de circuitos integrados básicos.
Así, si tenemos una función que se obtiene utilizando puertas AND y OR como se muestra en la figura 132, tiene la desventaja de necesitar dos tipos diferentes de circuitos integrados.
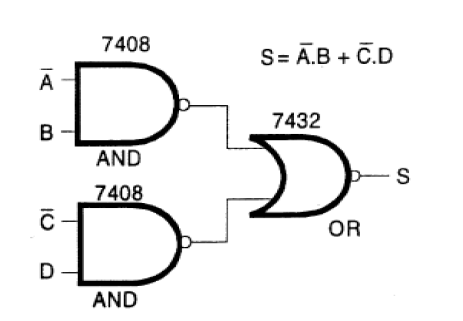
Si queremos esta función con circuitos TTL, por ejemplo, aprovecharemos tres de tres puertas de 3 entradas de un circuito 7411, y también tenemos que disfrutar de uno de los cuatro o puertas de dos entradas de un circuito integrado 7432.
Por supuesto, vamos a utilizar dos circuitos integrados perdiendo 1/3 de uno y 3/4 de la otra.
Podemos simplificar considerablemente este circuito si utilizamos sólo puertas NAND con la configuración equivalente que se muestra en la figura 133.
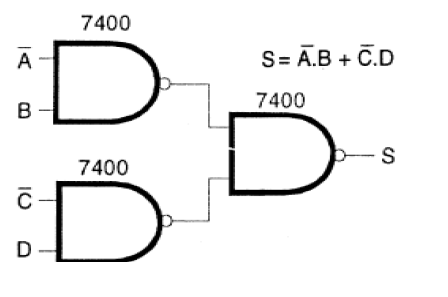
Este circuito, que tiene la misma función que el anterior, utiliza las tres puertas de un circuito integrado 7410. El resultado final es que sólo usamos un circuito integrado, que está completamente pinchado, sin ninguna parte ociosa.
Vea que es importante considerar esta posibilidad en un proyecto comercial donde el número de componentes, y su costo, son factores importantes para su implementación.
5.5 – Diagramas Karnaugh
Un proceso muy interesante de representar una tabla verdad, y de él para obtener una simplificación de los circuitos usados para su implementación, es lo que hace uso de los llamados diagramas Karnaugh o mapas.
El diagrama Karnaugh consiste en una tabla rectangular con un número de fotogramas que corresponde a 2 elevados al exponente N, donde N es el número de variables en el circuito.
Cada variable lógica ocupa el gráfico la mitad de su longitud, y su complemento ocupa la otra mitad.
En la figura 134 se muestra cómo se elaboran los diagramas Karnaugh para 1, 2 y 3 variables, con las expresiones lógicas correspondientes a cada caso.
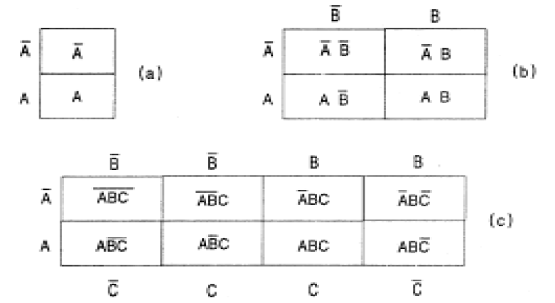
Vea que para 1 variable, tenemos 2 casas; para 2 variables, 4 casas y para 3 variables, 8 casas.
Las expresiones lógicas, asociadas a cada cómic, se obtienen de una manera muy similar a la utilizada en el conocido juego de "Batalla naval" donde la posición de cada "disparo" se da por dos coordenadas, una correspondiente a las líneas y la otra a las columnas.
En la figura 135 se muestra, como ejemplo, cómo se puede obtener un diagrama Karnaugh de 4 variables con la inclusión dentro de cada fotograma de la expresión correspondiente.
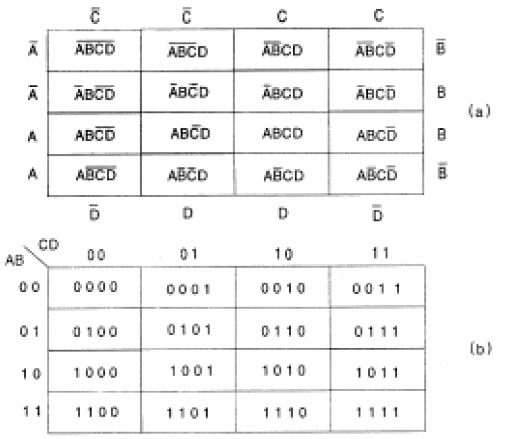
En el diagrama (b) de la figura 123, los marcos se rellenaron con los valores 0 y 1 correspondientes a las entradas. Este diagrama también se llama diagrama Veitch.
Una observación importante que se puede hacer en relación a esta representación por 0 y 1, es que cada fotograma difiere de la adyacente en un solo dígito. Decimos que son adyacentes a los términos que están a la derecha y a la izquierda de cada fotograma y también a los que están por encima y por debajo. También son adyacentes a los que están en la misma cola, pero uno en la primera columna y el otro en el último.
En la figura 136 tenemos un mapa con la identificación de los adyacentes.
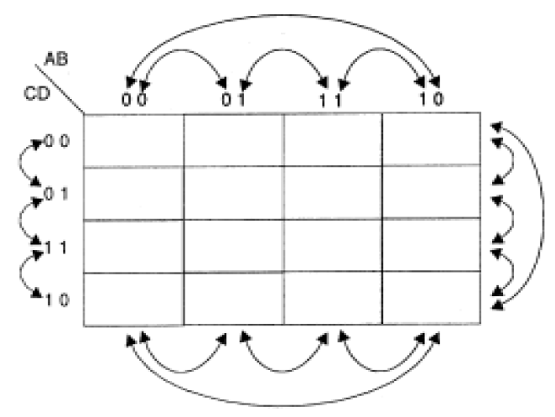
Por lo tanto, para hacer las simplificaciones, lo que hacemos es trazar la tabla verdad de la función que deseamos implementar en un mapa Karnaugh. Con esto, será posible identificar mejor las adyacencia, y así hacer las simplificaciones que conducen al uso mínimo de funciones lógicas en la implementación de un circuito.
Para que el lector entienda cómo "funciona" el mapa de Karnaugh en una simplificación de una función, vamos a tomar como ejemplo una función relativamente simple, función que se da por la siguiente tabla verdad:
A B S
0 0 1
0 1 1
1 0 0
1 1 1
Deseamos expresar esta tabla como una suma de productos, lo que significa que los valores adyacentes que debemos buscar en la tabla son los "1". Si tuviéramos que expresar esta función como el producto de una suma, los valores considerados serían el "0", y el procedimiento final sería el mismo.
A continuación, construimos el diagrama Karnaugh para esta tabla como se muestra en la figura 137.
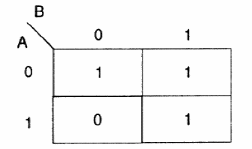
A partir de este diagrama, nuestro siguiente paso es tratar de hacer simplificaciones que puedan conducir a circuitos más simples en la implementación.
El identificador Es entonces para agrupar los términos adyacentes, que son iguales, y hay varias posibilidades que se muestran en la figura 138.
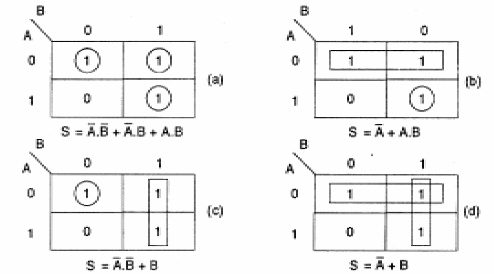
La primera posibilidad que se muestra en (a) conduce a una suma de tres productos, cada uno obtenido por la intersección de la línea con la columna donde se encuentra el "1" correspondiente.
Así que el primero está en la columna que intercepta A-0 con B-0. Ahora, el valor cero en la indexación indica la inversión, por lo que esto significa que el primer factor de nuestro producto será:
/A. /B
El segundo "1" que se considerará está en la columna A = 1 y B = 0 , por lo tanto tenemos A invertido y B sin inversión, lo que nos lleva al segundo factor de nuestro producto:
/A. B
Finalmente, el tercer "1" a considerar es en la línea A = 1 y B = 1 que significa un factor con A, multiplicado por B sin inversión o:
A. B
¿Cómo debemos expresar la función en forma de una suma de productos que hacemos:
S = /A. /B + A. /B + A. B
Para el segundo caso (b), tenemos una mayor simplificación ya que agrupamos los dos "1" de la primera línea para que podamos adoptarlo:
/A
Para el otro valor "1" que se encuentra en la casa que corresponde a la intersección de A = 1 con B = 1 vale la suma (sin inversión):
A + B
La expresión final en la forma de un producto de sumas es entonces:
S = /A + B. A
Del mismo modo, hemos llegado a la simplificación (b) que permite obtener una expresión más simple, porque hemos logrado unir tres casas adyacentes.
Razonamiento de la misma manera que llegamos a la expresión:
S = /A + B
El procedimiento que vimos como ejemplo implicaba una simple función, con sólo dos variables de entrada. Sin embargo, exactamente el mismo procedimiento es válido para cualquier número de variables.
Los lectores interesados en profundizar deben tratar de entrenar los procedimientos indicados trabajando con funciones cada vez más complejas.
Los trabajos más avanzados, que se ocupan de la lógica digital, deben ser consultados para aquellos que deseen ir más allá, ya que el propósito de este curso es una introducción a la electrónica digital.
Existen otros métodos de simplificación como el Método Tabular de Quine-Mac Cluskey que son más apropiados para simplificar ecuaciones de más de 5 variables. Este método se recomienda para un alto número de variables, ya que el método Karnaugh se vuelve muy complicado de usar con más de 5 variables.
Sumário
Curso de Electrónica - Electrónica Digital (CUR5000)
Curso de Electrónica - Electrónica Digital – Parte 1 (CUR5001S)
Curso de Electrónica Digital – Parte 2 - El Álgebra de Boole (CUR5002S)
Curso de Electrónica - Electrónica Digital - Parte 6 - Los Elementos Biestables (CUR5006S)
Curso de Electrónica - Electrónica Digital - Parte 9 - Contadores Digitales (CUR6002S)




