El osciloscopio es uno de los instrumentos de gran utilidad en el taller del técnico reparador, del proyectista y también del ingeniero, pues proporciona la visualización precisa de las formas de las ondas y fenómenos transitorios. En este primer artículo de la serie abordamos el uso del osciloscopio en el taller, tratando básicamente la medida de tensiones y la verificación de fases.
Mediante el osciloscopio podemos visualizar formas de onda y otros fenómenos transitorios que ocurren en un circuito electrónico.
El osciloscopio tiene por base un tubo de rayos catódicos (TRC) que está conectado a una serie de circuitos que permiten que se opere con él c señales en una amplia gama de frecuencias e intensidades. (figura 1)

Este artículo es de 1988. Hoy tenemos osciloscopios con pantallas de cristal líquido y mismo tipos digitales.
EI sistema de barrido que opera con seriales en "diente de Sierra" permite "congelar" las imágenes correspondientes a los fenómenos repetitivos tales como formas de ondas, y así facilitar eI análisis que efectúa el técnico. (figura 2)
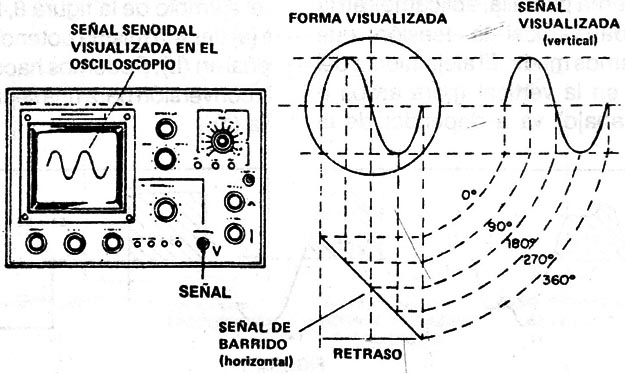
Vea en la figura 2 que la com- binación de señal diente de sierra del barrido del osciloscopio, con una señal sinodal de entrada da por resultado una imagen que el retrato" de la señal sinodal.
Para el técnico es muy importante saber analizar una imagen reproducida en la pantalla de un osciloscopio pues ella corresponde a lo que está sucediendo en el circuito electrónico. A veces, por la simple observación de una deformación (distorsión) o de un corte, el técnico puede llegar inmediatamente al componente o componentes que presentan problemas.
En el caso de un amplificador, el osciloscopio además de permitir la visualización de cualquier distorsión en las frecuencias que se emplean, permite también ia medida de la potencia, sensibilidad y otras características importantes. (figura 3)

Sabemos que no todos los técnicos reparadores pueden poseer un osciloscopio en sus talleres, pero sin duda los que invirtieran capital en este equipo, en poco tiempo lo recuperarían con ganancia debido al tiempo que ganarían en el trabajo y a la precisión de los arreglos.
Para un técnico reparador de radios o TV, los osciloscopios con frecuencias máximas de hasta 15MHz son satisfactorios para la mayoría de los trabajos.
EI Único problema para el técnico que no está familiarizado con el instrumento es aprender en poco tiempo todas las aplicaciones prácticas del mismo, ya que son muy numerosas.
MEDIDA DE TENSIONES
Las pantallas de los osciloscopios vienen calibradas con un reticulado de modo que, en función de las ganancias seleccionadas para los circuitos internos, podemos usarlas como referencia para medir tensiones.
Es así que, si la llave selectora de ganancia estuviera en la posición de 1V/div, lo que corresponde a 1 volt por cada división, bastará centrar la señal para poder obtener diversas informaciones sobre su intensidad a partir de la forma de onda.
En la figura 4 tenemos ejemplos de señales con 1,5V de tensión de pico, o 3Vpp (volts de pico a pico) si la llave está en la posición de 1 V por división, y 25V de pico ó 50V pico a pico con la llave en la posición de 10V por división.

Supongamos que en los dos casos el técnico sepa hacer la conexión del osciloscopio al circuito en ensayo para obtener las formas de ondas.
En el caso de un oscilador por ejemplo, el procedimiento puede ser el de la figura 5 (oscilador de audio).

Se ajusta la frecuencia de barrido y se sincroniza para poder obtener una imagen estacionaria.
Es claro que antes de aplicar la señal debemos "centrar" el trazo como muestra la figura 6.

Vea que este procedimiento no se aplica únicamente a señales alternadas.
También las tensiones continuas pueden medirse con el osciloscopio. Una vez centrado el trazo en la pantalla, aplicamos en la entrada vertical la tensión que queremos medir. El alejamiento del trazo en la vertical (para arriba o para abajo) va a depender de la tensión de entrada. En la figura 7 tenemos un ejemplo en el que medimos una tensión continua de 5V con el osciloscopio.

Si la señal analizada tiene forma de onda conocida - sinodal, triangular, rectangular-. además de los valores de pico, resulta fácil obtener otros valores como por ejemplo el valor medio, el valor rms. Del mismo modo, si se trata de una serial de audio de forma conocida, también podemos calcular la potencia.
Si la serial tuviera una forma más compleja, sólo con su análisis podremos calcular el valor rms o sea el valor medio. Para eso debemos "copiar" la figura que aparece en la pantalla del osciloscopio y calcular su área.
Para el ejemplo de la figura 8, la señal en (a) tiene la misma potencia quela señal en (b). Podemos hacer la misma conversión para una señal cuadrada (c).

Para medir la potencia de un amplificador de audio debemos hacer Ias conexiones que se muestran en la figura 9.

Entonces a partir de la aplicación de una señal sinodal en la entrada y con una carga resistiva que corresponda en valor a la impedancia menor admitida para los altoparlantes,- podemos determinar la tensión de pico, la tensión rms y hasta la tensión media. (figura 10)

A partir de la fórmula:
P = V2/R
Donde:
P es la potencia en watts.
V es la tensión (de pico, media o rms según Ia potencia calculada) en volts.
R es la resistencia de carga.
Para el técnico reparador, un osciloscopio de trazo único que no tenga memoria ni microprocesador, ya es de enorme importancia.
Saber usarlo es un recurso profesional de los más significativos.
Calculamos la potencia y también podemos visualizar distorsiones eventuales.
En la figura 11 tenemos algunos tipos de deformaciones de una señal de onda cuadrada de entrada y su interpretación para un amplificador de audio.

Vea que siempre debemos usar carga resistiva, pues la carga inductiva tiene un comportamiento que introduce deformaciones en la forma de la onda analizada.
Existen osciloscopios modernos, sofisticados, que en sus circuitos incorporan microprocesadores y otros circuitos que permiten la medida y visualización (y hasta memorización) de las características de las señales observadas. Al mismo tiempo que aparece en la pantalla la forma de onda de la señal, tenemos indicaciones proyectadas de su frecuencia, amplitud, fase, etc.
Otros osciloscopios, y estos son más comunes, poseen doble trazo es decir, un barrido múltiple que permite visualizar dos formas de onda al mismo tiempo. (figura 12)

VERIFICACIÓN DE FASE
Si aplicamos a las entradas (vertical y horizontal) de un osciloscopio, dos señales de amplitudes cercanas y la misma frecuencia, el resultado será una imagen única paralizada en la pantalla. Deberá desconectarse el barrido interno para efectuar este análisis. (figura 13)

La Imagen, para el caso de señales sinusoidales, podrá ir desde un trazo inclinado hasta un circulo (para señales de la misma frecuencia) como se ve en la figura 14.

La figura formada es el resultado de la combinación o composición de movimientos armónicos simples (MAS) que puede ser prevista con facilidad mediante fórmulas matemáticas.
Solamente tendremos circunferencias en el caso de que las dos señales estén en cuadratura, o sea con una diferencia de fase de 90 ó 270 grades.
Los valores intermedios pueden calcularse teniendo como base la graduación (cuadriculado) de la pantalla del osciloscopio. Para el caso de la figura 15 bastará medir las dos dimensiones mostradas ("a" y "b") y calcular el ángulo con la fórmula:
sen e = a/b

Consultando una tabla de senos y cosenos podemos encontrar con facilidad el valor del ángulo. Una calculadora que tenga la función arc sen o una microcomputadora, también permite el cálculo inmediato.
Es evidente que este procedimiento debe tener en cuenta la linealidad del circuito del osciloscopio, que no debe introducir ningún cambio de fase en las señales estudiadas.
CONCLUSIÓN
Vimos sólo dos aplicaciones posibles del osciloscopio. Todas constituirían un libro. Los lectores que deseen profundizar sus conocimientos del asunto deben consultar otros artículos de este sitio así como libros del autor.




