Los circuitos resonantes se encuentran en prácticamente todos los equipos de telecomunicaciones. Son responsables de la frecuencia de la señal que debe ser transmitida o recibida, por la separación de señales en filtros, por el rechazo de interferencias y ruidos y mucho más. En este artículo, explicamos cómo funciona este tipo de circuito.
Todos los objetos tienen una frecuencia de vibración. Percibimos esto cuando golpeamos una copa, un pedazo de metal o un diapasón. El material de que se hace el objeto, sus dimensiones y su formato determinan esta frecuencia. Denominamos esta frecuencia de "frecuencia de resonancia". Un hecho interesante puede ser observado cuando dos objetos cercanos tienen la misma frecuencia de resonancia y hacemos uno de ellos vibrar.
Dos diapasones afinados para la misma frecuencia, por ejemplo, pueden servir de ejemplo para un experimento interesante que involucra este hecho. Cuando golpeamos en un emisor de sonido, este sonido hace que el otro diapasón entre en vibración. Podemos percibir esto acercando el oído del segundo diapasón, como muestra la figura 1.
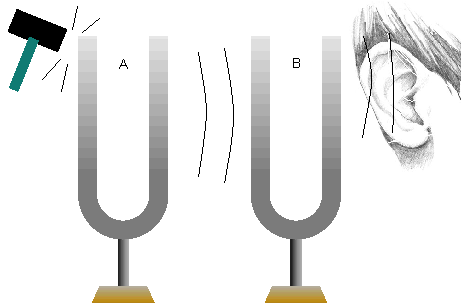
Este fenómeno también ocurre con los circuitos electrónicos. Determinados circuitos electrónicos también poseen frecuencias propias de vibración, emitiendo señales en una sola frecuencia cuando son excitados. Y, circuitos similares que reciben estas frecuencias tienden a vibrar de forma más intensa, recibiendo las señales de estas frecuencias. En el caso, el circuito que hace esto es el circuito resonante LC mostrado en la figura 2.
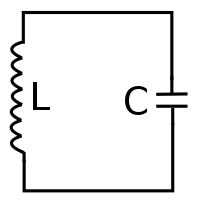
Este circuito presenta algunas propiedades de extrema importancia para las radiocomunicaciones. La primera de ellas es la de oscilar en una frecuencia única. Así, tomando el circuito básico de la figura 3, vamos a suponer que el capacitor esté completamente cargado.
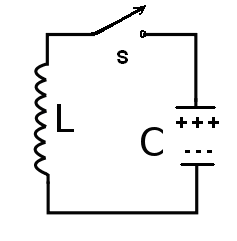
En estas condiciones iniciales, existe un campo eléctrico uniforme entre las armaduras del capacitor y en él está almacenada la energía del circuito.
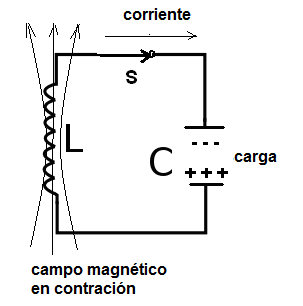
Cerrando el interruptor, una corriente de descarga del capacitor fluye a través del inductor. Con la descarga del capacitor la corriente creada crea un campo magnético que se expande hacia el cual se transfiere la energía, como muestra la figura 4.
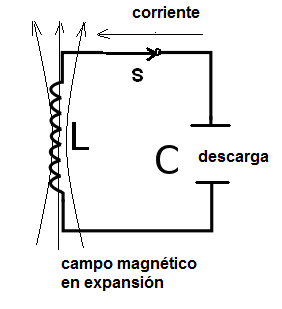
Cuando la corriente de descarga cesa, toda la energía está en el campo magnético del inductor. En este momento, el campo magnético empieza a contraerse induciendo en el inductor una tensión que carga el capacitor, pero con polaridad opuesta, como muestra la figura 5.
Terminada la contracción del campo, con su desaparición, el capacitor comienza ahora a descargarse nuevamente, pero con una corriente opuesta a la inicial. Esta corriente genera un nuevo campo magnético invertido que se expande en el inductor, como muestra la figura 6.
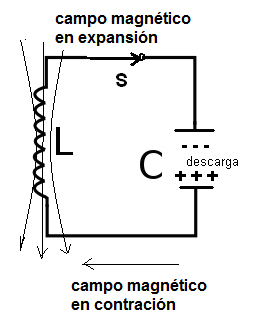
Una vez más, con la descarga completa del capacitor y el campo magnético en el máximo, se inicia una nueva contracción con una nueva carga del capacitor con la polaridad original. Un nuevo ciclo como el descrito tiene entonces inicio.
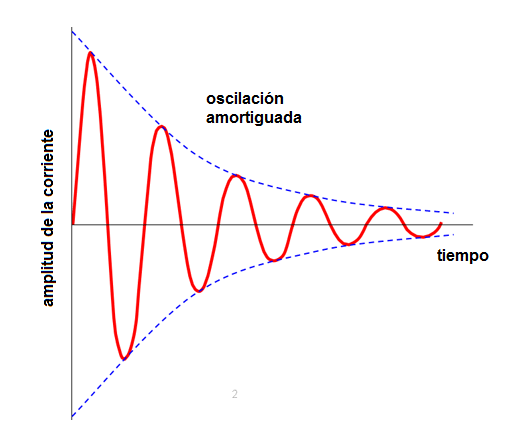
Si la carga y descarga del capacitor no ocurría con pérdidas el ciclo ocurrir por tiempo infinito generando así una señal senoidal cuya frecuencia dependería de los valores del capacitor y del inductor. En la práctica, sin embargo, los conductores del inductor y del circuito representan una resistencia que absorbe energía. Así, la oscilación que ocurre es amortiguada hasta desaparecer, como muestra la figura 7.
Si en cada ciclo producido la energía perdida es restablecida, tendremos una señal de amplitud constante. Esto se puede lograr a través de circuitos amplificadores, como ocurre en los denominados osciladores. En un oscilador tenemos un componente (válvula o transistor) que constantemente repone la energía perdida en cada oscilación manteniendo así su intensidad constante. En realidad, hasta restaura energía más de modo que parte de ella pueda ser aprovechada en un circuito externo, como muestra la figura 8.
Cuando un circuito LC se excita él oscila en una frecuencia que depende del inductor y del capacitor.
Sin embargo, si la excitación es otra señal ocurre un fenómeno importante dado por la resonancia. Si la frecuencia de la señal excitante es diferente de la frecuencia natural de oscilación, o sea, de la frecuencia de resonancia, tendrá dificultad en acompañar las variaciones de esta señal, y con ello su impedancia será reducida. En estas condiciones, el circuito se comporta como un conductor para la señal que pasará a través de él, como muestra la figura 9.
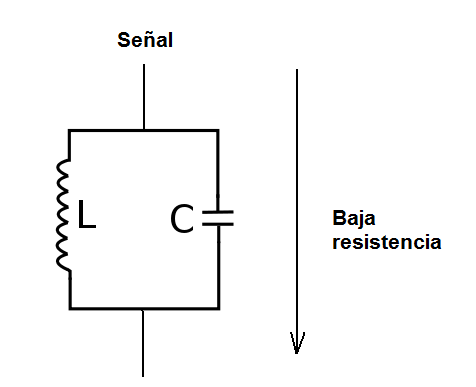
Sin embargo, si la frecuencia de la señal coincide con la frecuencia de resonancia del circuito LC, se comportará como un circuito de alta impedancia, apareciendo entonces la señal en sus extremos con gran amplitud, como muestra la figura 10.
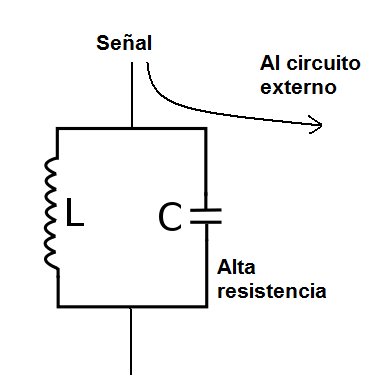
Esta característica se aprovecha en los circuitos de sintonía de los receptores. En la entrada de un receptor de radio, los circuitos resonantes LC paralelos permiten que sólo señales de una determinada frecuencia aparezcan en sus extremos y sean enviados a los circuitos de procesamiento, mientras que los demás son cortocircuitados para la tierra, como muestra la figura 11.
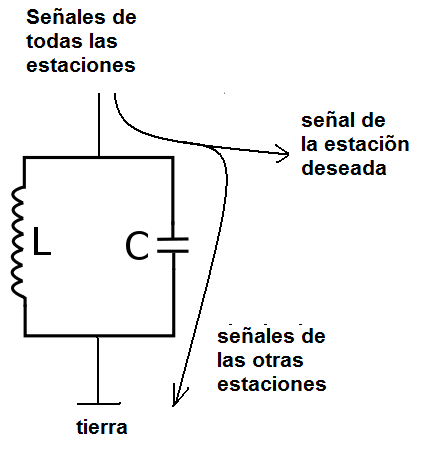
En la práctica es común que el capacitor sea variable de modo que una cierta banda de frecuencias sea barrida y así seleccionadas las estaciones deseadas. Esto ocurre con los receptores simples.
Una posibilidad explorada en los circuitos de sintonización LC consiste en utilizar un capacitor de estado solido cuya capacitancia puede ser controlada por la tensión, o sea, un diodo de capacitancia variable o varicap, en un circuito como el de la figura 12.
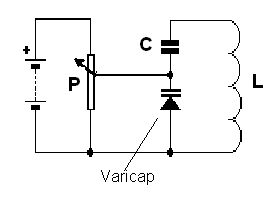
En este circuito, la tensión aplicada al diodo de capacitancia variable determina su capacitancia y así la frecuencia sintonizada por el circuito. Esta configuración permite que los microcontroladores y otros dispositivos de estado sólido se utilizan para realizar la sintonización automática de estaciones de un circuito.
Pero, los circuitos resonantes también pueden ser formados por un capacitor y un inductor conectados en serie, como muestra la figura 13.
En estos circuitos en la frecuencia de resonancia la impedancia presentada es baja, mientras que en las demás, la impedancia es alta.
Selectividad - Factor Q
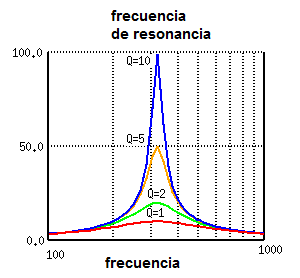
Si analizamos los circuitos resonantes, en la condición ideal, ellos deberían responder sólo a una determinada frecuencia, rechazando las demás. En la práctica, sin embargo, la presencia de resistencias parásitos en el circuito hace que él tiende a tener curvas de respuestas menos agudas, lo que determina el factor de calidad o factor Q, que mide su selectividad. Así, como muestra la figura 14, un circuito con un factor de calidad más elevado, tiene una selectividad mayor, responde mejor a una determinada frecuencia y rechazando las demás.
Sin embargo, en la práctica, no debemos tener un circuito de sintonía cuya selectividad sea máxima, pues eso también va a significar que, en la modulación de la señal recibida, cuando se desplaza de su frecuencia, tendremos su pérdida.
El factor Q es dado por la fórmula:
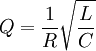
Dónde:
Q es el factor Q
R es la resistencia asociada al circuito en ohms
C es la capacitancia en las farads
L es la inductancia en henry
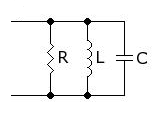
En la figura 15 tenemos el circuito equivalente con la resistencia asociada:
Conclusión
Lo que hemos visto es sólo un poco sobre el funcionamiento de los circuitos resonantes. Podemos aprender mucho más, analizando cómo se utilizan en osciladores y receptores. Este tema se puede encontrar otros artículos de nuestra sección de Telecom en este sitio.




