Este artículo nos enseñan cómo funciona el contador binario desde el conocimiento del funcionamiento de lo flip-flop en otro artículo del sitio.
Vamos a suponer un multivibrador biestable en él en el disipador de los transistores que corresponde a la salida, encendemos un LED, como se muestra en la figura 1.
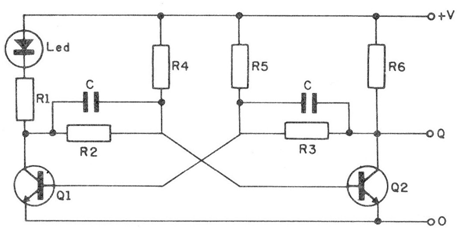
En estas condiciones, podemos asociar al transistor en conducción y el LED encendido en un valor binario, que por la convención puede ser 1. (Nota: que no tenemos que tomar la tensión en el colector en este caso como 1, el mismo resultado final, si obtiene de adoptáramos 0 y seguimos hasta el final, con el fin de la operación, el resultado final será el mismo).
De esta manera, asociamos al multivibrador activado el LED enciende y desactivado el LED apagado:
LED encendido = 1
LED apagado = 0
Hacemos entonces la conexión de 4 flip-flops en serie, como se muestra en la figura 2.
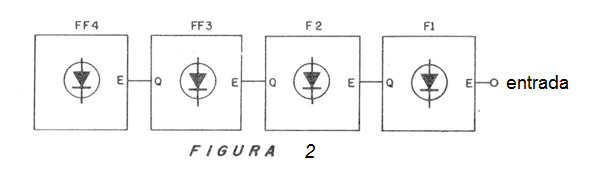
Salimos de la situación inicial en todos los LED están apagados, es decir, los multivibradores en situación estable correspondiente a 0000 (que en decimal representa el número 0).
Representamos esta situación como se muestra en la figura 3.
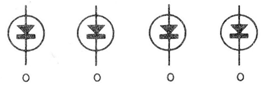
Al se aplicar un primer pulso negativo en la entrada de este circuito, el primer flip-flop cambia de estado, haciendo su LED, inicialmente apagado, encender.
Entonces tendremos la presentación del número binario 0001 que corresponde precisamente a la decimal 1 (vea figura 4).
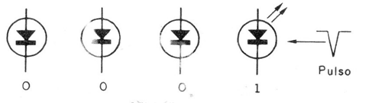
Vea que el segundo flip-flop no cambiará de estado porque la transición en la salida del primer flip-flop fue de cero a uno, y esto sólo puede responder a una transición de 1 a 0.
Ahora viene el siguiente pulso de numero 2, los flip-flop cambia de estado otra vez, va de 1 a 0. El LED se apaga, pero la transición en la salida es negativa y esto hace que el segundo flip-flop cambie de estado. Su LED, inicialmente apagado enciende y tenemos la representación 0010. Esto corresponde a la "2" en binario. (Vea figura 5).
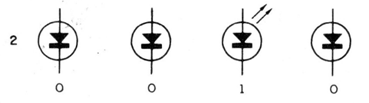
Vea que el tercer flip-flop no cambia de estado, porque en el segundo tenemos una transición de 0 a 1 que él no responde.
Ahora viene el tercer pulso. Otra vez el primer flip-flop cambia de estado de 0 a 1. El segundo no cambia, la transición fue positiva de 0 a 1, lo mismo ocurriendo con el tercero.
Entonces tenemos representación 0011, que precisamente corresponde al binario 3.
La representación puede verse mejor en la figura 6.
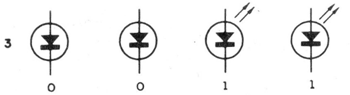
Ahora viene el cuarto pulso. El primer flip-flop cambia nuevamente de estado, va de 1 a 0. Una transición negativa ocurre que es sentida por el segundo flip-flop que también cambia de estado, va de 1 a 0. El tercer flip-flop, en presencia de una transición negativa cambia de estado y pasa de 0 a 1. El paso de 0 a 1 no afecta al cuarto flip-flop que se mantiene en su situación de 0.
Tenemos la situación que corresponde a 0100 "4" en binario (ver figura 7).
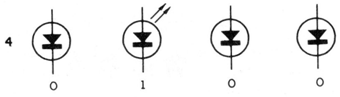
En la figura 8, tenemos lo que ocurre en pulsos sucesivos hasta 16 cuando el sistema se "reinicia", es decir, después de alcanzar su capacidad máxima de la cuenta de nuevo al estado inicial.

Como el lector puede averiguar, con 4 Flip-flop puede contar hasta16 o 24.
Véase también que, si aplicamos 3 pulsos en el circuito y luego otras 5, el sistema acumulará 8 pulsos y presenta el resultado de la suma 3 + 5 = 8 en binario. Este circuito, por esta razón también recibe el nombre de acumulador y puede ser utilizado en la realización de sumas.
BCD o Decimal Codificado en Binario
Las representaciones que hemos visto fueran en binario puro y estamos acostumbrados a trabajar con números decimales.
Sin embargo, si agrupamos los 3 flip-flop podemos contar solamente hasta 8, cuando la base es 10, y agrupamos 4 flip-flops pasamos de 10, puesto que pudimos contar hasta 16.
Para adaptar un sistema a lo otro existe el código BCD en que hemos establecido los valores binarios que corresponden a los números decimales y estas son sólo 10.
Así, tenemos el código BCD que es dada por:

Así, para escribir el número 78 en BCD hacer:
0111 1000
El número 235 será:
0010 00110101
En Ciencias de la Computación es común aprovechar más 6 valores binarios que se representan por:
1 0 1 0 A
1 0 1 1 B
1 1 0 0 C
1 1 0 1 D
1 1 1 0 E
1 1 1 1 F
Así que cuando un programa en ensamblador o en "lenguaje máquina" tecleando F5 lo que entra en los circuitos de lógica es: 1111 0101.
Hay otros códigos que le permiten traducir información en binario, decimal como Octal, pero estos no deben todavía ser estudiados para no "complicar" la vida del lector por lo menos por un tiempo.



